A heuristic model for predicting scalability and chances of success for startups, small businesses, or new ventures.
No one can predict the future, at least not yet! However, there is a lot to learn from Mother Nature, as I have written about in my other articles (e.g., flocking behavior, genetic algorithms) to derive lessons learned and applications for your business strategy. If we can’t learn from Mother Nature for our business strategies — where else can we look?
Fractals are yet another mathematical concept from nature that has shown promise in business applications.
You may be wondering whether the business you are getting into (or already have) will scale successfully. Or you may be an entrepreneur, a venture capitalist, an angel investor, or the CEO of a large enterprise, who constantly evaluates and assesses whether to invest in a new venture.
You may have done your own financial forecasts and calculated your NPVs and IRRs, or you may be evaluating someone else’s. We all know how often such financials are far from reality when all is said and done. In fact, nine times out of 10, forecasts and predictions on paper never materialize in real life.
Let us say you are in a hurry, and you don’t want to dive deep into the analysis. You just want a heuristic method to predict the future viability of the venture.
In this article, I will introduce and explain the concept of fractals, and I’ll provide a simple method for testing your business for scalability success.
What are Fractals?
A fractal is a shape made out of parts that are similar to the whole in some way. Think of a fractal as an object that is “self-similar” or “scalable.” A fractal is made out of both smaller and larger copies of itself. Classic examples of fractals which are found in nature include coastlines, trees, snowflakes, etc.
Several German and French mathematicians introduced Fractals over a century ago, including Felix Hausdorff, Paul Levy, Pierre Fatou, Waclaw Sierpinski, and Gaston Julia.
Then, in 1975, a mathematician named Benoit Mandelbrot introduced fractal geometry.
To visualize fractals, think of objects in nature: For example, a cauliflower. When you cut off a branch, you will see that it’s made out of smaller branches, and the branch itself is part of other similar branches that make the larger cauliflower. Each fractal subcomponent is smaller than the former and has the same scalable shape and structure, exhibiting the power law effect.

Mandelbrot demonstrated how a simple formula with a feedback loop could lead to a complex system.
The most important takeaway here is that a fractal exhibits power-law behavior and that a fractal is not an either-or category. Instead, objects are either more or less fractal-like.
Mandelbrot demonstrated that 1) a simple formula with a feedback loop can lead to a complex system that exhibits power-law behavior, and 2) fractals are not an either-or category; objects or systems are more or less fractal-like. The philosopher Charles S. Peirce contends that every object in the universe is a continuum because a continuum “is something whose possibilities of determination no multitude of individuals can exhaust.” What is a continuum, if not a fractal?
Benoit Mandelbrot was the first thinker to show how markets exhibited power-law characteristics due to fractal-like behavior. You can read all about it in his book The Misbehavior of Markets.
What Does a Fractal Market Mean?
What is groundbreaking here is — if the stock market exhibits fractal properties — what about individual stocks? If stock markets are fractal-like, this would also mean that individual stocks are self-similar. And this concept means that business units, organizations, and large or small enterprises can be considered fractals. It turns out that even stocks themselves exhibit fractal behavior, as shown by M. Warusawitharana (2016) in Time-Varying Volatility and the Power Law Distribution of Stock Returns.
By some amazing feature of the unity of science, these scaling laws seem to work across the board, from fractal geometry to biology, to geophysics, to the spreading of ideas, to the distribution of wealth and artistic success.
These “self-similar” laws were first mentioned by Pareto in economics in the distribution of income as early as the 19th century. Yule later rediscovered these laws in biology. And last, we have shown how they apply to index funds, the stock market, and individual stocks. The self-similarity principle applies to any company or business of any size and is even narrowed down to a single employee.
In fact, from supply chains to innovations and organization structures, they all exhibit power-law behavior. Below is a list of things that have been researched to exhibit power-law behavior:
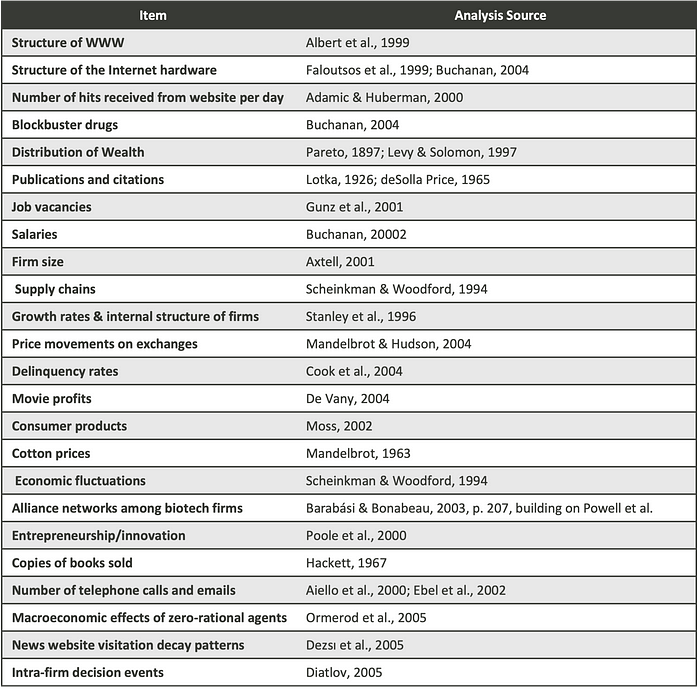
What are Power Laws?
If you are not yet familiar with power laws, the best way to illustrate them is in their distribution. Power-law distributions — sometimes referred to as Zipf’s law — are different from binomial and normal distributions in terms of the shape of the curve, where the latter follow the shape of a “bell” curve and have an average, power-law distributions have no averages and are said to have long tails that extend indefinitely (also sometimes referred to as heavy-tailed distributions), and they decay much slower than exponential distribution; that is the key feature that makes anything that follows a power-law distribution unpredictable.
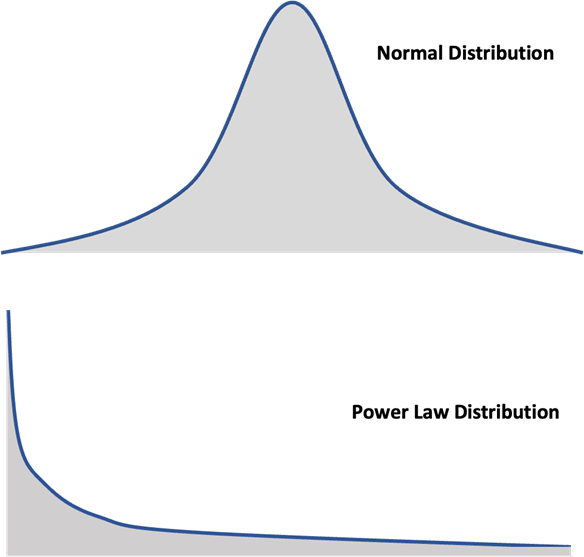
Empirical data published by Clauset, Shalizi, and Newman (2009) shows how power-law distributions occur in dozens of real-world examples, including the distribution of wealth, words, wars, the internet, the evolution of species, book sales, cities, religions, etc.
A distinctive feature of power-law curves is that when plotted on a scattered log-log plot, the graph looks like a downward sloping curve, almost like a straight line.

Fractals Litmus Test to Predict the Future of Your Business
Now, let us take the proof that Mandelbrot offered on the fractal property of stock markets and consider it in reverse.
Say you are looking at a new venture. You have to plan how this venture would look in the future (i.e., 3–7 years down the line). You have to build a vision of this future in your mind. Then, you ask yourself the following questions as you try to visualize your venture:
- How will the business operate?
- Are there identifiable or real markets (and customers) for products or services at all scales and geographies?
- Are there identifiable operations on a significant scale?
- Are there freestanding alternatives with a comparable scale?
- Can the business be structured for an IPO?
Which of the below dimensions will help the business grow? (Note that it can be multiple)
Now, with this vision of the future and the growth dimension(s) of your venture in mind, let us recap what constitutes self-similarity and fractal-like behavior. Note that I emphasize fractal-like because most objects in nature are not perfectly fractal but rather exhibit fractal-like behavior. Because something is generally — rather than absolutely — true does not mean it cannot be used as a heuristic. Indeed, a heuristic implies that the information it indexes is only generally true; otherwise, we would not have a heuristic, and we would have facts.
- The first characteristic is self-similarity: Is the venture self-similar? If a business is not self-similar, then it is not fractal. Note that self-similarity is not perfect self-similarity but rather, contains a fractal dimension (perfect self-similarity is only theoretical).
- The second characteristic is the power law: Does your venture exhibit power-law behavior? If you recall, fractals must exhibit power-law behavior, and if a business does not exhibit power-law behavior, then it is not fractal.
Adopting these two principles to your future venture vision, how will the future company pan out? If you answer “no” to any of the above, you may need to think twice before jumping on to investing in the business.
In Conclusion
There are no guarantees that this method can — with absolute certainty — predict the future (no one can), but the idea is: Fractals can be a good indication and a potential alarm for those who adopt it.
Considering fractals as a heuristic, one cannot help but wonder if fractals in nature can be demonstrated to exist in the stock market from the top-down, would they not also exist from the bottom-up in a mature business?
I cannot think of a better method to predict future business success than the heuristics of fractals.
References
Clauset, A, Shalizi, C.R., & Newman, M.E.J. (2009). Power law distributions in empirical data. Siam Review 51(4), 661–703.
Zamaleo, F. (2012). Peirce’s Logic of Continuity. Boston: Docent Press.

